miércoles, 8 de diciembre de 2010

MATRICES

MATRICES

Las matrices aparecen por primera vez hacia el año 1850, introducidas por J.J. Sylvester
El desarrollo inicial de la teoría se debe al matemático W.R. Hamilton en 1853
En 1858, A. Cayley introduce la notación matricial como una forma abreviada de escribir un sistema de m ecuaciones lineales con n incógnitas.

Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales. Además de su utilidad para el estudio de sistemas de ecuaciones lineales, las matrices aparecen de forma natural en geometría, estadística, economía, informática, física, etc...

La utilización de matrices (arrays) constituye actualmente una parte esencial dn los lenguajes de programación, ya que la mayoría de los datos se introducen en los ordenadores como tablas organizadas en filas y columnas : hojas de cálculo, bases de datos,...

CONCEPTO DE MATRIZ

Una matriz es un conjunto de elementos de cualquier naturaleza aunque, en general, suelen ser números ordenados en filas y columnas.

Se llama matriz de orden "m × n" a un conjunto rectangular de elementos a_ij dispuestos en m filas y en n columnas. El orden de una matriz también se denomina dimensión o tamaño, siendo m y n números naturales.

Las matrices se denotan con letras mayúsculas: A, B, C, ... y los elementos de las mismas con letras minúsculas y subíndices que indican el lugar ocupado: a, b, c, ... Un elemento genérico que ocupe la fila i y la columna j se escribe a_ij . Si el elemento genérico aparece entre paréntesis también representa a toda la matriz : A = (a_ij)

Cuando nos referimos indistíntamente a filas o columnas hablamos de lineas.
El número total de elementos de una matriz Am×n es m·n
En matemáticas, tanto las Listas como las Tablas reciben el nombre genérico de matrices.

Una lista numérica es un conjunto de números dispuestos uno a continuación del otro.

MATRICES IGUALES

Dos matrices A = (a_ij)m×n y B = (b_ij)p×q son iguales, sí y solo si, tienen en los mismo lugares elementos iguales, es decir :

ALGUNOS TIPOS DE MATRICES

Hay algunas matrices que aparecen frecuentemente y que según su forma, sus elementos, ... reciben nombres diferentes :

Tipo de matriz	Definición	Ejemplo
FILA	Aquella matriz que tiene una sola fila, siendo su orden 1×n
COLUMNA	Aquella matriz que tiene una sola columna, siendo su orden m×1
RECTANGULAR	Aquella matriz que tiene distinto número de filas que de columnas, siendo su orden m×n ,
TRASPUESTA	Dada una matriz A, se llama traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas. Se representa por A^t ó A^T
OPUESTA	La matriz opuesta de una dada es la que resulta de sustituir cada elemento por su opuesto. La opuesta de A es -A.
NULA	Si todos sus elementos son cero. También se denomina matriz cero y se denota por 0m×n
CUADRADA	Aquella matriz que tiene igual número de filas que de columnas, m = n, diciendose que la matriz es de orden n. Diagonal principal : son los elementos a₁₁ , a₂₂ , ..., a_nn Diagonal secundaria : son los elementos a_ijcon i+j = n+1 Traza de una matriz cuadrada : es la suma de los elementos de la diagonal principal tr A.	Diagonal principal : Diagonal secundaria :
SIMÉTRICA	Es una matriz cuadrada que es igual a su traspuesta. A = A^t , a_ij= a_ji
ANTISIMÉTRICA	Es una matriz cuadrada que es igual a la opuesta de su traspuesta. A = -A^t , a_ij= -a_ji Necesariamente a_ii = 0
DIAGONAL	Es una matriz cuadrada que tiene todos sus elementos nulos excepto los de la diagonal principal
ESCALAR	Es una matriz cuadrada que tiene todos sus elementos nulos excepto los de la diagonal principal que son iguales
IDENTIDAD	Es una matriz cuadrada que tiene todos sus elementos nulos excepto los de la diagonal principal que son iguales a 1. Tambien se denomina matriz unidad.
TRIANGULAR	Es una matriz cuadrada que tiene todos los elementos por encima (por debajo) de la diagonal principal nulos.
ORTOGONAL	Una matriz ortogonal es necesariamente cuadrada e invertible : A^-1 = A^T La inversa de una matriz ortogonal es una matriz ortogonal. El producto de dos matrices ortogonales es una matriz ortogonal. El determinante de una matriz ortogonal vale +1 ó -1.
NORMAL	Una matriz es normal si conmuta con su traspuesta. Las matrices simétricas, antisimétricas u ortogonales son necesariamente normales.
INVERSA	Decimos que una matriz cuadrada A tiene inversa, A-1, si se verifica que : A·A^-1 = A^-1·A = I

Para establecer las reglas que rigen el cálculo con matrices se desarrolla un álgebra semejante al álgebra ordinaria, pero en lugar de operar con números lo hacemos con matrices.

OPERACIONES CON MATRICES

SUMA DE MATRICES

La suma de dos matrices A = (a_ij)m×n y B = (b_ij)p×q de la misma dimensión (equidimensionales) : m = p y n = q es otra matriz C = A+B = (c_ij)m×n = (a_ij+b_ij)

Es una ley de composición interna con las siguientes
PROPIEDADES :

· Asociativa : A+(B+C) = (A+B)+C
· Conmutativa : A+B = B+A
· Elem. neutro : ( matriz cero 0_m×n ) , 0+A = A+0 = A
· Elem. simétrico : ( matriz opuesta -A ) , A + (-A) = (-A) + A = 0
Al conjunto de las matrices de dimensión m×n cuyos elementos son números reales lo vamos a representar por M_m×n y como hemos visto, por cumplir las propiedades anteriores, ( M, + ) es un grupo abeliano.

¡¡ La suma y diferencia de dos matrices NO está definida si sus dimensiones son distintas. !!

PRODUCTO DE UN NÚMERO REAL POR UNA MATRIZ
Para multiplicar un escalar por una matriz se multiplica el escalar por todos los elementos de la matriz, obteniéndose otra matriz del mismo orden.

Es una ley de composición externa con las siguientes
PROPIEDADES :

PRODUCTO DE MATRICES
Dadas dos matrices A = (a_ij)m×n y B = (b_ij)p×q donde n = p, es decir, el número de columnas de la primera matriz A es igual al número de filas de la matriz B , se define el producto A·B de la siguiente forma :

El elemento aque ocupa el lugar (i, j) en la matriz producto se obtiene sumando los productos de cada elemento de la fila i de la matriz A por el correspondiente de la columna j de la matriz B.

MATRIZ INVERSA

Se llama matriz inversa de una matriz cuadrada An y la representamos por A^-1 , a la matriz que verifica la siguiente propiedad : A^-1·A = A·A^-1 = I

Decimos que una matriz cuadrada es "regular" si su determinante es distinto de cero, y es "singular" si su determinante es igual a cero.

PROPIEDADES :

Sólo existe matriz inversa de una matriz cuadrada si ésta es regular.

La matriz inversa de una matriz cuadrada, si existe, es única.

Entre matrices NO existe la operación de división, la matriz inversa realiza funciones análogas.

MÉTODOS PARA HALLAR LA MATRIZ INVERSA :

Aplicando la definición

Por el método de Gauss

Por determinantes

Gauss-Jordan.

Algoritmo de Gauss-Jordan.
Se denomina matriz escalonada a una matriz en la que las filas posteriores
a una fila cuyos elementos son todos ceros, tienen todos sus elementos igual
a cero, y el n´umero de elementos nulos al comienzo de cada fila no nula es
estrictamente menor que en la siguiente.
Teorema 1.1 Dada una matriz cualquiera A 2 Rm×n existen matrices F y
U tales que FA = U siendo U una matriz escalonada.
Demostraci´on. Probaremos el teorema de forma constructiva.
a) Si a11 6= 0, mediante transformaciones elementales filas Fij( ) podemos
anular todos los elementos de la primera columna, salvo el a11. Estas
transformaciones ser´ıan de la forma Fi1(−
ai1
a11
).
b) Si a11 = 0 y alg´un elemento de la primera columna es no nulo, podemos
llevarlo al lugar (11) mediante una transformaci´on Fij y proceder despu´es
como en el caso anterior.
c) Si ai1 = 0 8 i = 1, . . . , m, la primera columna es de ceros y por tanto,
ai1 = 0 8 i > 1, es decir, se trata de una columna del tipo de las matrices
escalonadas.
Procedemos despu´es con a22 (el elemento a22 resultante de las transformaciones
anteriores) al igual que procedimos con a11 anteriormente, es decir, si a22 6= 0
lo utilizamos para hacer ceros por debajo de ´el en la segunda columna. Si
fuese a22 = 0 vemos si existe por debajo de ´el alg´un elemento ai2 6= 0 y, en
caso de haberlo, realizamos la transformaci´on F2i, etc.
Reiterando el proceso, llegamos a una matriz escalonada U. La matriz F
no es m´as que el producto de las matrices de las transformaciones elementales
filas realizadas para pasar de A a U.
El siguiente organigrama, muestra el algoritmo de escalonamiento de una
matriz A 2 Rm×n, mediante transformaciones elementales filas. Cuando se
alcanza la condici´on de parada, la nueva matriz A es escalonada.
Algoritmo de Gauss-Jordan. 11
Algoritmo de escalonamiento de una matriz.
Ejemplo 1.7 Consideremos la matriz A del Ejemplo 1.1.
A
F21(−2)
−!
0
@
2 1 3 4
0 0 −5 −3
1 0 2 3
1
A F31(−1
2 )
−!
0
@
2 1 3 4
0 0 −5 −3
0 −1/2 1/2 1
1
A F23 −!
0
@
2 1 3 4
0 −1/2 1/2 1
0 0 −5 −3
1
A = U
siendo U una matriz escalonada. Dado que
E23E31(−
1
2
)E21(−2)A = U =) FA = U
con
F = E23E31(−
1
2
)E21(−2) =
0
@
1 0 0
0 0 1
0 1 0
1
A
0
@
1 0 0
0 1 0
−1/2 0 1
1
A
0
@
1 0 0
−2 1 0
0 0 1
1
A )
12 Matrices y determinantes
F =
0
@
1 0 0
−1/2 0 1
−2 1 0
1
A

Se denomina forma escalonada can´onica a una matriz escalonada con la
propiedad de que el primer elemento no nulo de una fila es un uno y adem´as,
es el ´unico elemento no nulo de su columna.
Teorema 1.2 Toda matriz puede ser reducida mediante transformaciones elementales
fila a una escalonada can´onica.
Demostraci´on. Basta con observar que una vez obtenida la matriz U, si en
una fila hay alg´un elemento no nulo, la dividimos por el primer elemento no
nulo de ella mediante Fi( ) y lo utilizamos para hacer ceros todos los de su
columna (que se encontrar´an por encima de ´el).
Ejemplo 1.8 En el Ejemplo 1.7 se vi´o que
A −! U =
0
@
2 1 3 4
0 −1/2 1/2 1
0 0 −5 −3
1
A F1( 1
2 )
−!
0
@
1 1/2 3/2 2
0 −1/2 1/2 1
0 0 −5 −3
1
A F2(−2)
−!
0
@
1 1/2 3/2 2
0 1 −1 −2
0 0 −5 −3
1
A F12(−1
2 )
−!
0
@
1 0 2 3
0 1 −1 −2
0 0 −5 −3
1
A F3(−1
5 )
−!
0
@
1 0 2 3
0 1 −1 −2
0 0 1 3/5
1
A
F13(−2)
−!
0
@
1 0 0 9/5
0 1 −1 −2
0 0 1 3/5
1
A F23(1)
−!
0
@
1 0 0 9/5
0 1 0 −7/5
0 0 1 3/5
1
A
que se trata de una escalonada can´onica.
Los elementos que utilizamos para anular a los dem´as elementos de una
columna se denominan pivotes. Si en un determinado paso del proceso de
pasar de A a U alguna columna es de ceros, diremos que el correspondiente
pivote es nulo.
Teorema 1.3 Toda matriz A 2 Rm×n puede, mediante transformaciones elementales,
transformarse en una del tipo

Ir 0
0 0

Algoritmo de Gauss-Jordan. 13
teniendo en cuenta que para ello es necesario realizar tanto transformaciones
fila como transformaciones columna.
Ejemplo 1.9 Si nos fijamos en la matriz del Ejemplo 1.7 que transformamos,
mediante transformaciones elementales fila (ver Ejemplo 1.8) en la escalonada
can´onica 0
@
1 0 0 9/5
0 1 0 −7/5
0 0 1 3/5
1
A
podemos ahora, mediante la composici´on de las transformaciones columna
C41(−9
5 )C42( 7
5 )C43(−3
5 ) llevarla a
0
@
1 0 0 0
0 1 0 0
0 0 1 0
1
A =
􀀀
I3 | 0

.
Teorema 1.4 Una condici´on necesaria y suficiente para que una matriz cuadrada
posea inversa es que su forma escalonada can´onica sea la matriz unidad.
Demostraci´on. Si su forma escalonada can´onica es In, existe F 2 Rn×n tal
que FA = In =) F = A−1.
Si existe A−1 tal que A−1A = In =) 9 F = A−1 tal que FA = In y por
tanto, In es la forma escalonada can´onica de A.
Este teorema nos permite calcular la matriz inversa, de una matriz dada,
mediante transformaciones elementales (filas o columnas, pero no ambas simult
´aneamente), es decir, aplicando el Algoritmo de Gauss-Jordan tomando
como matriz inicial(A | In)
Ejemplo 1.10 Consideremos la matriz A =
0
@
1 3 0
0 1 1
1 2 0
1
A
(A | I3) =
0
@
1 3 0 1 0 0
0 1 1 0 1 0
1 2 0 0 0 1
1
A F31(−1)
−!
0
@
1 3 0 1 0 0
0 1 1 0 1 0
0 −1 0 −1 0 1
1
A F12(−3)
−!
0
@
1 0 −3 1 −3 0
0 1 1 0 1 0
0 −1 0 −1 0 1
1
A F32(1)
−!
0
@
1 0 −3 1 −3 0
0 1 1 0 1 0
0 0 1 −1 1 1
1
A F13(3)
−!
14 Matrices y determinantes
0
@
1 0 0 −2 0 3
0 1 1 0 1 0
0 0 1 −1 1 1
1
A F23(−1)
−!
0
@
1 0 0 −2 0 3
0 1 0 1 0 −1
0 0 1 −1 1 1
1
A =)
A−1 =
0
@
−2 0 3
1 0 −1
−1 1 1
1
A
ya que: F23(−1)F13(3)F32(1)F12(−3)F31(−1)(A) = I3 =)
[E23(−1)E13(3)E32(1)E12(−3)E31(−1)]A = I3 =)
0
@
−2 0 3
1 0 −1
−1 1 1
1
AA = I3 )
A−1 =
0
@
−2 0 3
1 0 −1
−1 1 1
1
A

1.5 Determinante de una matriz cuadrada.
Los determinantes nos proporcionan un m´etodo para el c´alculo de la matriz
inversa de una dada (en caso de existir) y un criterio para estudiar si una
matriz es o no invertible.
Sus aplicaciones son m´ultiples en todas las ramas de las ciencias que tratan
problemas lineales en los que necesariamente aparecen matrices y por tanto,
determinantes.
1.5.1 Definiciones.
Sea A = (aij) una matriz cuadrada de dimensi´on n. A cada matriz cuadrada
A se le asigna un n´umero real que llamaremos determinante de A y representaremos
por det(A) o |A|. Su c´alculo se obtiene mediante la siguiente f´ormula
recurrente sobre el tama˜no n:
• para n = 1 ! A = (a11), se define det(A) = a11
• para n > 1 ! det(A) =
Xn
i=1
akiAki

Proyecciones Ortogonales: Proceso de Gram-Schmidt

Proceso de ortogonalización de Gram-Schmidt

De Wikipedia, la enciclopedia libre

Saltar a navegación, búsqueda

En álgebra lineal, el proceso de ortogonalización de Gram–Schmidt es un algoritmo para construir, a partir de un conjunto de vectores de un espacio prehilbertiano (usualmente, el espacio euclídeo Rⁿ), otro conjunto ortonormal de vectores que genere el mismo subespacio vectorial.

Este algoritmo recibe su nombre de los matemáticos Jørgen Pedersen Gram y Erhard Schmidt.

Descripción del algoritmo de ortogonalización de Gram–Schmidt

Los dos primeros pasos del proceso de Gram–Schmidt

Se define, en primer lugar, el operador proyección mediante

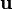$\mathrm{proj}_{\mathbf{u}}\,\mathbf{v} = {\langle \mathbf{v}, \mathbf{u}\rangle\over\langle \mathbf{u}, \mathbf{u}\rangle}\mathbf{u} = {||\mathbf{v}|| ||\mathbf{u}||\cos\alpha \over ||\mathbf{u}|| ||\mathbf{u}||1}\mathbf{u} = ||\mathbf{v}||\cos\alpha {\mathbf{u} \over ||\mathbf{u}||},$

donde los corchetes angulares representan el producto interior. Es evidente que

$\mathbf{v}-\mathrm{proj}_{\mathbf{u}}\,\mathbf{v}$

es un vector ortogonal a $\mathbf{u}$ . Entonces, dados los vectores 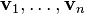$\mathbf{v}_1, \dots, \mathbf{v}_n$ , el algoritmo de Gram–Schmidt construye los vectores ortonormales $\mathbf{e}_1, \dots, \mathbf{e}_n$ de la manera siguiente:

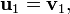
	$\mathbf{u}_1 = \mathbf{v}_1,$		$\mathbf{e}_1 = {\mathbf{u}_1 \over \|\|\mathbf{u}_1\|\|}$
	$\mathbf{u}_2 = \mathbf{v}_2-\mathrm{proj}_{\mathbf{u}_1}\,\mathbf{v}_2,$		$\mathbf{e}_2 = {\mathbf{u}_2 \over \|\|\mathbf{u}_2\|\|}$
	$\mathbf{u}_3 = \mathbf{v}_3-\mathrm{proj}_{\mathbf{u}_1}\,\mathbf{v}_3-\mathrm{proj}_{\mathbf{u}_2}\,\mathbf{v}_3,$		$\mathbf{e}_3 = {\mathbf{u}_3 \over \|\|\mathbf{u}_3\|\|}$
	$\vdots$		$\vdots$
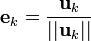
	$\mathbf{u}_k = \mathbf{v}_k-\sum_{j=1}^{k-1}\mathrm{proj}_{\mathbf{u}_j}\,\mathbf{v}_k,$		$\mathbf{e}_k = {\mathbf{u}_k\over\|\|\mathbf{u}_k\|\|}$

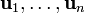A partir de las propiedades de la proyección y del producto escalar, es sencillo probar que la sucesión de vectores $\mathbf{u}_1, \dots, \mathbf{u}_n$ es ortogonal.

Ejemplo

Considera el siguiente conjunto de vectores en R² (con el convencional producto interno)

$S = \left\lbrace\mathbf{v}_1=\begin{pmatrix} 3 \\ 1\end{pmatrix}, \mathbf{v}_2=\begin{pmatrix}2 \\2\end{pmatrix}\right\rbrace.$

Ahora, aplicamos Gram–Schmidt, para obtener un conjunto de vectores ortogonales:

$\mathbf{u}_1=\mathbf{v}_1=\begin{pmatrix}3\\1\end{pmatrix}$

$\mathbf{u}_2 = \mathbf{v}_2 - \mathrm{proj}_{\mathbf{u}_1} \, \mathbf{v}_2 = \begin{pmatrix}2\\2\end{pmatrix} - \mathrm{proj}_{({3 \atop 1})} \, {\begin{pmatrix}2\\2\end{pmatrix}} = \begin{pmatrix} -2/5 \\6/5 \end{pmatrix}.$

Verificamos que los vectores u₁ y u₂ son de hecho ortogonales:

$\langle\mathbf{u}_1,\mathbf{u}_2\rangle = \left\langle \begin{pmatrix}3\\1\end{pmatrix}, \begin{pmatrix}-2/5\\6/5\end{pmatrix} \right\rangle = -\frac65 + \frac65 = 0.$

Entonces podemos normalizar los vectores dividiendo por su norma como hemos mostrado anteriormente:

$\mathbf{e}_1 = {1 \over \sqrt {10}}\begin{pmatrix}3\\1\end{pmatrix}$

$\mathbf{e}_2 = {1 \over \sqrt{40 \over 25}} \begin{pmatrix}-2/5\\6/5\end{pmatrix} = {1\over\sqrt{10}} \begin{pmatrix}-1\\3\end{pmatrix}.$